Last update: 22/11/2004
Problèmes
Voici quelques problèmes (sujet de recherche) proposé par Monsieur Doyen:
Question 1: 20points (Plus d'exam.)
Trouver une forme plus simple et plus courte de l'expression:
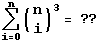comme par exemple: 
Question 2: 20points (Plus d'exam.)
De combien de façons différentes peut-on remplir une matrice m*n (pour tout m,n >0) avec des domino 1 * 2:
Exemple avec une matrice 2*n:
2*1 = 1 
2*2 = 2
ou 
2*3 = 3
ou
ou
On peut terminer de 2 façons (voir 2*2):
Donc si on pose un = 2*n ici 2*3, on voit ainsi que:
un = un-1 + un-2
=
+ 
On a ainsi trouvé la récurrence, que l'on peut résoudre.
Ici la solution est simple car un= Fn+1 ( Fn+1 est le n+1ème nombre de Fibonacci.)
Formule pour tout m*n (pour tout n,m >0) vaut 20 points
Formule pour un m*n (pour un m donné, et n > 6 avec démonstation) vaut 3 points
Résultats personnels
Résultats connus du problème numéro 2:
Ordre |
Equation |
Explications |
Prouvé |
Chercheur |
| 1*n | un = 1 | n=2*k ("k appartenant à Î N*) | / | / |
| 2*n | un = un-2 + un-1 | C'est un fibo. (Voir démo.) | oui | / |
| 3*n | oui | ..... | ||
| 4*n | oui | Ancien étudiant | ||
| 5*n | oui | Ancien étudiant | ||
| 6*n | un = un-1 + 20 un-2 + 10 un-3 - 38 un-4 - 10 un-5 + 20 un-6 - un-7 - un-8 | oui | Moi même | |
| 7*n | un = un-1 + 20 un-2 + 10 un-3 - 38 un-4 - 10 un-5 + 20 un-6 - un-7 - un-8 * | non | Moi même | |
| 8*n |
Un = un-1 + 76 un-2 + 69 un-3 – 921 un-4 – 584 un-5 + 4019 un-6 + 829 un-7 – 7010 un-8 + 829 un-9 + 4019 un-10 – 584 un-11 – 921 un-12 + 69 un-13 + 76 un-14 + un-15 - un-16 * |
non | Moi même |
* Ces résultats ne sont pas encore mathématiquement prouvés, et peuvent donc être erronés.
Si la recherche vous tentes (ou tout simplement des points sup.) alors contactez moi. Il reste encore assez de travail. Comme prouver le 7*n, 8*n...